Physics is all about understanding 2D and 3D images in all forms and how various factors affect the motion and movement of components. An important part of understanding the movement of 3D objects is to know about gradient divergence and curl. Now the question is, how to understand the physical significance of gradient divergence and curl and how to apply it with various properties? You need to understand the components of gradient, divergence, and curl and how you can affect the flow and movement of things related to the same.
What is the Physical Meaning of Gradient Divergence and Curl?
To understand the physical significance of gradient divergence and curl, you need to focus on the core property of Physics. Imagine a ball in your hand and a series of arrows towards the ball perpendicularly on the surface.
These are called gradients on the ball. In the case of irregular surfaces, divergence and curl occur simultaneously on the surface. Make sure that you understand how the 3D features of an image are very different from a plain 2D image. Only then will you understand the real significance of the same.
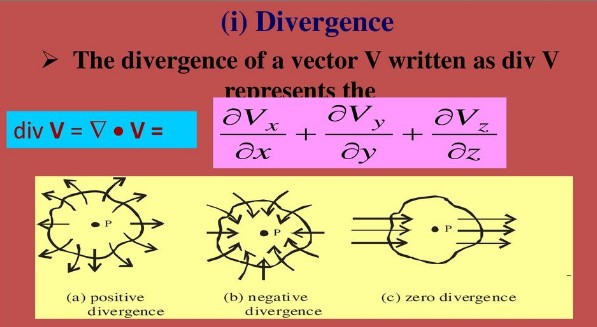
Divergence
Divergence refers to the change of flow of fluids Across a surface due to several reasons. For example, when water flows through a pipe, and several smaller pipes continue adding to the flow of water, it is called divergence.
If the initial flow is more than the final flow of water, then divergence is positive. On the other hand, if the initial flow is less than the final flow of water, then divergence is considered negative. It depends on whether the fluid flow has increased or decreased on the final surface.
Curl
Curl refers to the amount of rotation a fluid undergoes through a vector motion. For example, when you fill a cup with water, you will see that water does not settle on the cup with a linear motion.
Rather, it starts swirling upwards with a rotational motion by settling on the cup gradually. When the flow is in an anticlockwise motion, the curl is considered to be positive. On the other hand, when the flow is in a clockwise motion, the curl becomes negative.
Conclusion
Understanding the physical significance of gradient, divergence, and curl is very important to discover any defect and correct the disadvantages in due time. For example, if divergence becomes negative, then the flow of water will decrease on the final surface. If you want to correct this, you need to check the divergence with the correct gradient force. Similarly, if you want to increase the curl on a vector field, you need to make some changes to influence the rotation of the fluid at the right time. It is a very important topic in computational fluid dynamics (CFD), where you need to understand the correct direction and quantity of force applied on a given surface. In this way, you will be able to make changes to the gradient diversions and curl for the best results.